Rupture Propagation for Stochastic Fault Models
The dynamic propagation of rupture during an earthquake is essentially based on the friction law and on the stress spatial distribution at the initiation of the rupture process. The simulations, presented on this web page, show that the rupture process is not only very sensitive to the random properties of the stress spatial distribution but that these properties will affect the rupture path as well as the radiated energy generated in the process (Favreau et al, 2004; see also Peyrat et al., 2002 for a discussion about rupture propagation dependency onto the stress spatial distribution).
Two stochastic models of prestress distributions are considered. They are respectively based on Cauchy and Gaussian random variables. The parameters of the two stochastic models have values corresponding to the values computed for the slip distribution of the 1979 Imperial Valley earthquake (see Lavallee and Archuleta, 2003 for the stochastic model, and Archuleta, 1984 for the computation of the source model). We use a finite difference code to simulate the spontaneous propagation of shear rupture on a flat fault in a 3D continuum elastic body (see Figure 1 and the discussions in Favreau et al., 2002; and Favreau and Archuleta, 2003). The friction law is the slip dependent friction law (Figure 2).
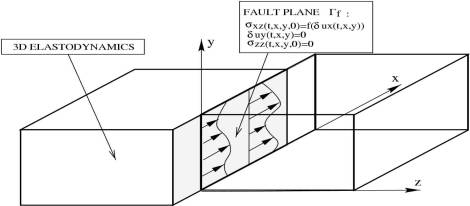
Figure 1: The two blocks represent the crust and have identical homogeneous density, shear modulus and Poisson ratio. The boundary conditions are the followings: absorption everywhere except at the contact of the blocks (the fault), where a slip dependent friction law is used to model the resistance of the fault (see Figure 2). For the numerical simulations we use a velocity-stress finite difference technique. The fault is introduced through an additional degree of freedom: the slip discontinuity (or stress glut). The absorbing boundary conditions are implemented using perfectly matched layers. We set dimensionless values for the parameters, i.e. density, shear wave velocity are set to unity. Poisson ratio is set to 0.25. The discretization is chosen to achieve an accurate sampling of the rupture front (function of the friction law parameters). With these specifications, computation of the the simulations presented below took from 0.1 to 0.8 Gb of memory and less than 2 hours each on a AMD 2000+ workstation.
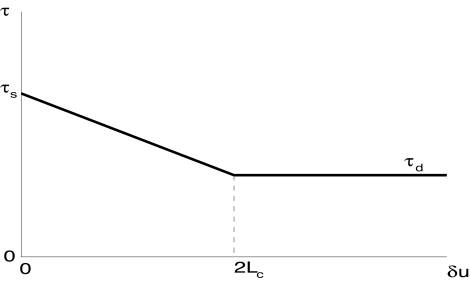
Figure 2: The friction law used is the basic slip dependent friction law. According to this law, the strength t decreases with the slip du from a maximal static strength ts to a residual dynamic strength td over a critical slip distance 2Lc. The parameter 2Lc determines also the negative slope of the friction law i.e. its weakening. In these simulations, the assumptions are symmetric blocks with no normal stress variations and that the heterogeneous slip over the fault has a constant rake. The dynamic friction is set to zero. The procedure is similar to the one discussed in Favreau and Archuleta (2003).
The effects described below are best observed by
watching the movie in slow motion.
Propagation of rupture conditioned by a Gaussian probability law: Rupture motion spreads smoothly from the nucleation center. Initially the rupture front is isotropic with respect to the nucleation point but at the end the motion is constrained into the strike direction. The shape of the rupture front is not very complex so few changes in the directivity can be expected once the rupture has spread over the full width of the model.
Propagation of rupture conditioned by a Cauchy probability law: The propagation of the rupture front is more complex. Note how the irregular shape of the rupture front after the initiation contrasts with the almost circular shape observed in the Gauss scenario, This may be related to the presence of a higher number of asperities in the Cauchy scenario. The second strong asperity has broken suddenly in one piece. It is nucleated by dynamic triggering, suggesting that the rupture progress trough "tunnel effect", i.e. the apparent rupture propagation was super-shear (on this issue see also Dunhan et al, 2003). This effect makes the rupture propagation faster than for the Gaussian model. Finally, note that due to quick change in the rupture motion observed in this case, directivity effect will be potentially stronger when compared to the smoother rupture of the Gauss scenario.
Additional information and suggested readings.
The formulation of the stochastic model of slip spatial heterogeneity introduced in Lavallee and Archuleta, 2003 and its applications to earthquake source models, as well as the consequences on ground motions are discussed in the following papers:
Another stochastic model of slip spatial heterogeneity based on the analysis of several earthquake source models is discussed in the following paper:
Mai, P. M., and G. C. Beroza. A spatial random-field model to characterize complexity in earthquake slip. J. Geophys. Res., 107, 2308, doi:10.1029/2001JB000588. 2002.
Examples of computed source models can be found at this web site:
http://seismo.ethz.ch/staff/martin/research/srcmod/srcmod.html
Acknowledgements: This research was supported by the following grants:
William Keck Interdisciplinary Program in Seismology and Materials Physics
Southern California Earthquake Center (SCEC).
References:
Archuleta, R. J. A Faulting model for the 1979 Imperial Valley earthquake. J. Geophys. Res., 89, 4559-4585, 1984
Dunham, E, Favreau, P, and Carlson, JM. A Supershear
Transition Mechanism for Cracks. Science,
299 , 1557-1559, 2003
Favreau, P., M. Campillo, and
I. R. Ionescu. Initiation of shear
instability in three-dimensional elastodynamics. J. Geophys. Res., 107, B7, 10.1029/2001JB000448, 2002.
Favreau, P., R. J. Archuleta and D. Lavallee,. In preparation for Geophys. Res. Lett., 2004.
Peyrat, S., K. Olsen, and R. Madariaga. Dynamic modeling of the 1992 Landers earthquake. J. Geophys. Res., 106, 26,467-236,482, 2002.